What are the key determinants of Toyota Corolla prices?

toyota corolla price analysis

*Group Project*

The price of a Toyota Corolla may vary for a wide variety of reasons. The following report examines the price of Toyota Corolla’s based on characteristics of the car.

The data analyzed includes age of purchaser, odometer reading in kilometers, fuel type required, horsepower, color, transmission type, displacement in cubic centimeters, number of doors, and weight of the car.

The primary objective of this analysis is to determine predictions regarding the Toyota Corolla sales price based on these variables. Through a regression analysis of the data, we were able to find that the primary drivers of price for manual transmission Corollas was Age, KM, FuelType, HP, CC, and Weight. On the other hand, for automatic transmission Corollas, the primary drivers included Age, KM, FuelType, CC, Doors, and Weight.

introduction

Through data analysis, we are able to analyze which features are most significant in determining the pricing of a Toyota Corolla.

The dataset used in this report consists of the following variables:

Price – The sales price of the Toyota Corolla (in Euros)
Age – Age of the purchaser
KM – Odometer reading in kilometers
FuelType – Fuel type (Diesel, Petrol or CNG)
HP – Horsepower
MetColor - Color
Automatic – Transmission (0 = Manual, 1 = Automatic)
CC – Displacement in cubic centimeters
Doors – Number of doors
Weight – Weight in kilograms

A scatter plot matrix is a useful tool in the initial inspection of a dataset. We constructed the graph below by coloring Price, Age, KM, and FuelType by the transmission variable. This scatterplot matrix provides interesting insight during the initial inspection of the variables in this dataset.

In the first graph, automatic transmission is represented with turquoise, and the manual transmission is colored as red. Because miles driven on a car exponentially decreases the car’s value, we can see in the scatterplot between price and KM that as the price of a car increases, the odometer reading decreases. Along with this, it is apparent that the relationship between price and age has a negative correlation. As someone’s age increases, they are less likely to purchase an expensive car. This can also be illustrated with the strong negative correlation -0.877 between age and price. In the second graph, this relationship is also demonstrated– regardless of whether the transmission was automatic or manual – although the automatic car trend line displayed overall higher average prices. Regarding the other variables, there does not appear to be significant correlations when coloring by type of transmission.

Regression model - manual

For the manual model, stepwise regression and best subsets were performed. We end up noticing that both MetColor and Doors turn out to be insignificant. The changes are minimal, resulting in our final model’s adjusted r-squared increasing from 0.8664 to only 0.8665.

Below is the final model.

The interpretation of the significant variables is as follows:

For every year increase in age, there will be a decrease of approximately 121.4 Euros keeping all other variables constant.
For every unit increase in kilometers, there will be a small decrease in price of .01674 Euros on average keeping all other variables constant.
If the fuel type is diesel, then the price will be increased by 3208 Euros assuming all variables are held constant.
If the fuel type is petroleum, then the price will be increased by 881.7 Euros on average keeping all other variables constant.
For every unit increase in HP (horsepower), the price increases by approximately 61.83 Euros if all variables are held constant.
For every increase in CC (displacement in centimeters), the price decreases by 4.046 Euros on average assuming all variables are held constant.
For every unit increase in weight, the price increases by approximately 19.41 Euros if all variables remain constant.

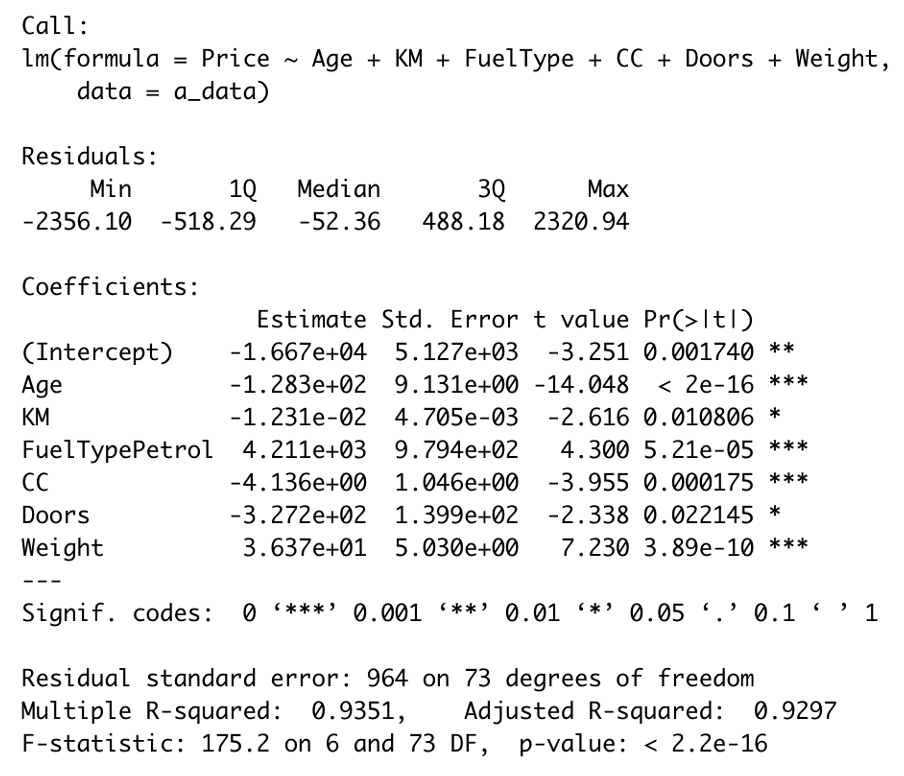
regression model - automatic

To see the significance of our variables for the automatic model, we performed stepwise regression. We end up with a slightly increased adjusted R-square from 0.9279 to 0.9297 with the better model.

We looked at the residuals and noticed some nonlinearity. We performed a log transformation which seemed to have helped the issue. Even though before performing the log transformation, our model had a higher adjusted r-squared and included only significant variables, we wanted to prioritize linearity, so we decided to stick with the transformed model. This model still has a high adjusted r-squared of 0.9159.

Below the final regression model.

The interpretation of the coefficients can be summed up as follows:

For every year increase in age, there will be a decrease of approximately .01090 Euros keeping all other variables constant.
For every unit increase in kilometers, there will be a small decrease in price of .000001168 Euros on average keeping all other variables constant.
If the fuel type is petroleum, then the price will be increased by .3635 Euros assuming all variables are held constant.
For every increase in CC (displacement in centimeters), the price decreases by .000182 Euros on average assuming all variables are held constant.
For every unit increase in doors, there is a decrease in price of .01828 Euros assuming all variables are held constant.
For every unit increase in weight, the price increases by approximately .001853 Euros if all variables remain constant.

Regression model - combined

To achieve the best model, stepwise regression was used to produce the combined model. However, upon inspection of the model, we noticed some nonlinearity that needed to be addressed, so we performed a logarithmic transformation.

Even though before performing the logarithmic transformation our model had a higher adjusted R-squared of 0.8685 and included only significant variables, we wanted to prioritize linearity, so decided to stick with the transformed model. This model maintains a high adjusted R-squared of 0.847.

The interpretation of the significant variables is as follows:

For every year increase in age, there will be a decrease of approximately .0154 Euros keeping all other variables constant.
For every unit increase in kilometers, there will be a small decrease in price of .000001683 Euros on average keeping all other variables constant.
If the fuel type is diesel, then the price will be increased by .08443 Euros assuming all variables are held constant.
If the fuel type is petroleum, then the price will be increased by .07642 Euros on average keeping all other variables constant.
For every unit increase in HP (horsepower), the price increases by approximately .002598 Euros if all variables are held constant.
If transmission is considered, automatic (manual is the reference group) cars have a higher cost of approximately .03827 Euros if all other variables are constant.
For every increase in CC (displacement in centimeters), the price decreases by .00004680 Euros on average assuming all variables are held constant.
For every unit increase in weight, the price increases by approximately .001086 Euros if all variables remain constant.

conclusion

When conducting this analysis, three regression models were developed to further examine the relationship between pricing and the predictor variables. We were able to determine from the results that as the price of a car increases, the odometer reading decreases, as well as when someone’s age increases, it is less likely that they will purchase an expensive car.

With the results of the manual, automatic, and combined model presenting high adjusted R-squares (0.8665, 0.9297, 0.847, respectively), we can conclude that the models provide an effective fit.